Mathematica可能是地表最强的数学软件，现在我们用它来解一下PDE。

PDE求解

以金融随机分析领域著名的BSM方程为例：

$\frac{\partial f}{\partial s}+\frac{\partial f}{\partial S}rS+ \frac{1}{2}\frac{\partial f}{\partial S}\sigma ^2 S^2=rf$

边界条件： $f(S,T)=max(S-X,0)$ 。

式中， $S$ 表示基础资产的价值，而 $t$ 自然是表示时间， $\sigma$ 表示基础资产的波动率，通常小于1， $r$ 为无风险利率， $f$ 表示期权价格， $X$ 为期权的执行价格，注意区分期权的价格与执行价格， $T$ 表示期权的到期时间，它的单位与波动率的单位相同，通常对于两者我们都以年为单位。在给定 $r, \sigma, T, X$ 的情况下通过求解这个方程，我们可以得到期权的价格关于基础资产价格 $S$ 与时间 $t$ 的函数。

在Mathematica中我们用以下代码求解这个方程:

r=0.1;sigma=0.3;T=0.25;

sol=DSolve[{D[f[S, t], t] + r S D[f[S, t], S] + 1/2 D[f[S, t], {S, 2}] sigma^2 S^2 == r f[S, t],
f[S, T] == Max[S – X, 0]}, f[S, t], {S, t}]

在输入这个方程时，有几点需要注意的地方：

方程中的函数名后一定要加参数，比如 $f[S,t]$ ，无论是不是偏导数，不要只写 $f$ 。
偏导数的形式为 $D[f[S,t],{S,2}]$ 表示对 $S$ 的2阶偏导数。
边界条件与主方程一起设定。
一定记住是 $==$ 而不要写成 $=$ ，后者是赋值运算。

注意在输入的方程中，我们没有设定 $X$ ，原因是运行时发现如果指定了 $X$ ，则方程解不出来。

得到以下结果（直接copy as Latex）：

$latex \left\{\left\{f(S,t)\to -0.487655 \left(e^{0.1 t} X \text{erfc}\left(\frac{1.17851 (-2 \log (S)+0.11 (t-0.25)+2 \log (X))}{\sqrt{0.25\, -t}}\right)-1.02532 S \text{erfc}\left(\frac{1.17851 (-2 \log (S)+0.29 (t-0.25)+2 \log (X))}{\sqrt{0.25\, -t}}\right)\right)\right\}\right\}$

可视化

用Plot3D可以进行可视化，对于X，我们可以用Manipulate动态展示：


c[S_, t_, X_] := Evaluate[f[S, t] /. sol];
Manipulate[Plot3D[c[S, t, X], {S, 0, X}, {t, 0, T}, AxesLabel -> Automatic,
PlotRange -> All], {{X, 40, "parameter"}, 30, 80,
Appearance -> "Labeled"}]

在Manipulate语句中用Apperance->”Labeled”来显示可变参数的数值。

结果如下：

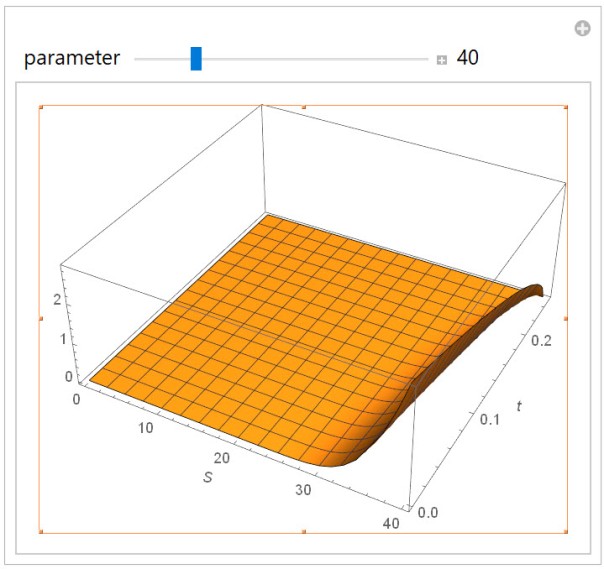
2017-08-28_23-43-52